1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
| from functools import reduce
import numpy as np
def pad_data(data):
""" 对输入数据进行 64-bit 块填充(PKCS7 填充) """
byte_data = data.encode('utf-8')
pad_len = 8 - (len(byte_data) % 8)
byte_data += bytes([pad_len] * pad_len)
return [int.from_bytes(byte_data[i:i+8], 'big') for i in range(0, len(byte_data), 8)]
def unpad_data(data_blocks):
""" 去除填充并转换回字符串 """
byte_data = b''.join(block.to_bytes(8, 'big') for block in data_blocks)
pad_len = byte_data[-1]
return byte_data[:-pad_len].decode('utf-8')
def int2bin(a, n):
assert 0<=n and a < 2**n
res = np.zeros(n, dtype = int)
for x in range(n):
res[n-x-1] = a % 2
a = a // 2
return res.tolist()
assert int2bin(0x1a, 10) == [0, 0, 0, 0, 0, 1, 1, 0, 1, 0]
def bin2int(a):
return reduce(lambda x,y: x*2+y, a)
assert bin2int([0, 0, 0, 0, 0, 1, 1, 0, 1, 0]) == 0x1a
def leftRotate(a, off):
return a[off:] + a[:off]
assert leftRotate([0, 1, 0, 1, 1], 2) == [0, 1, 1, 0, 1]
def binXor(a, b):
assert len(a) == len(b)
return [x^y for x, y in zip(a, b)]
assert binXor([1, 1, 0, 1], [0, 1, 1, 0]) == [1, 0, 1, 1]
def IP(a):
ip = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
return [a[x-1] for x in ip]
testM = [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1]
assert IP(testM) == [1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0]
def FP(a):
fp = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
return [a[x-1] for x in fp]
def PC1(key):
pc1_l = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36]
pc1_r = [63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]
return [key[x-1] for x in pc1_l], [key[x-1] for x in pc1_r]
testKey = [0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1]
testL, testR = PC1(testKey)
assert testL + testR == [1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1]
def PC2(key):
assert len(key) == 56
pc2 = [14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32]
return [key[x-1] for x in pc2]
def keyGen(key):
assert len(key) == 64
l, r = PC1(key)
off = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
res = []
for x in range(16):
l = leftRotate(l, off[x])
r = leftRotate(r, off[x])
res.append(PC2(l + r))
return res
assert keyGen(testKey)[-1] == [1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1]
def S(a):
assert len(a) == 48
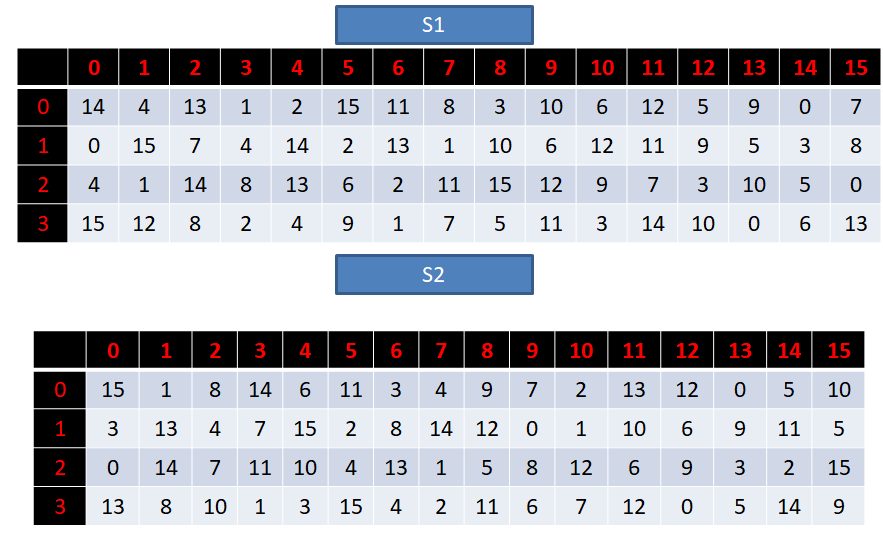
S_box = [[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13],
[15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9],
[10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12],
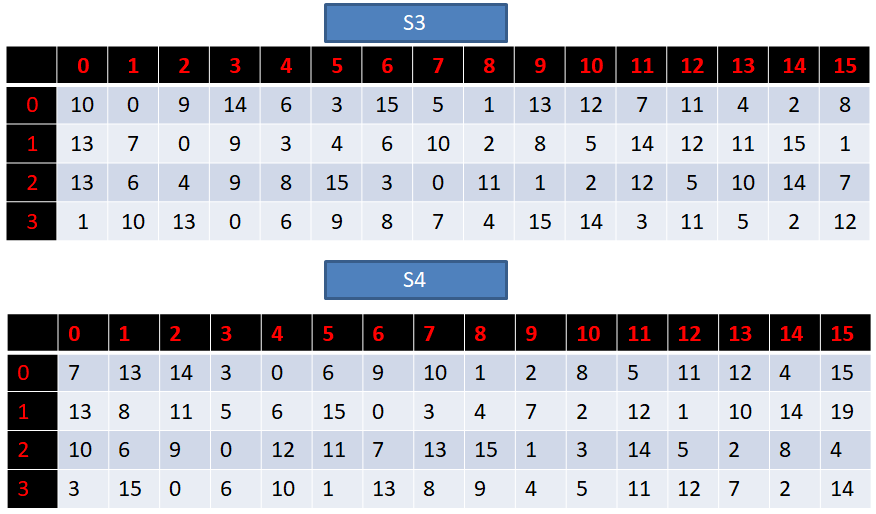
[7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14],
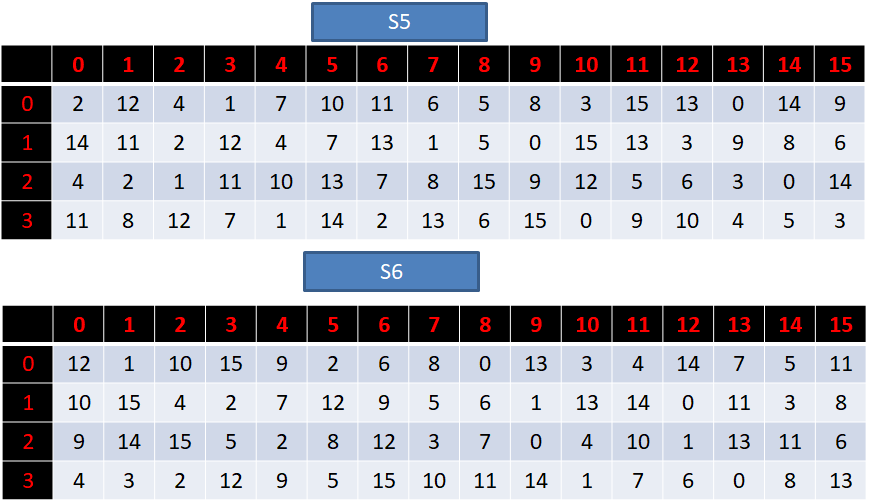
[2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3],
[12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13],
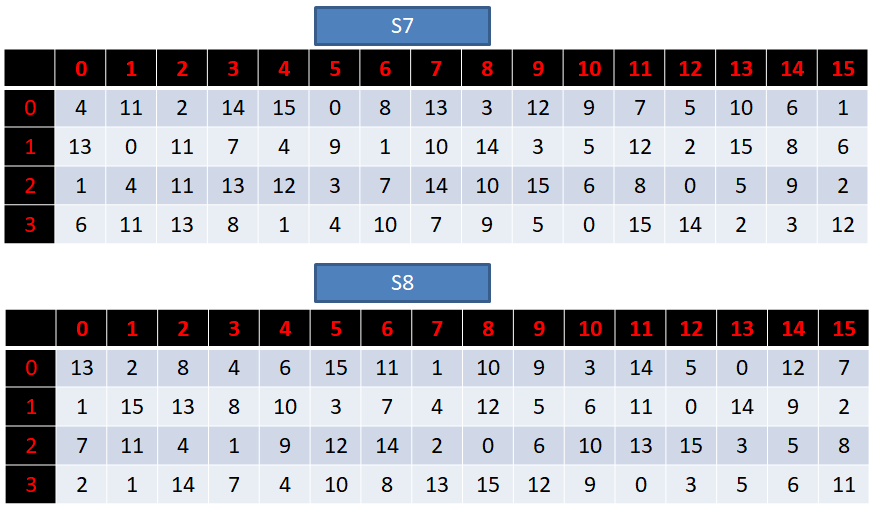
[4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12],
[13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11]]
a = np.array(a, dtype=int).reshape(8, 6)
res = []
for i in range(8):
p = a[i]
r = S_box[i][bin2int([p[0], p[5], p[1], p[2], p[3], p[4]])]
res.append(int2bin(r, 4))
res = np.array(res).flatten().tolist()
assert len(res) == 32
return res
def Expand(a):
assert len(a) == 32
e = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1]
return [a[x-1] for x in e]
def P(a):
assert len(a) == 32
p = [16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25]
return [a[x-1] for x in p]
def Feistel(a, subKey):
assert len(a) == 32
assert len(subKey) == 48
t = binXor(Expand(a), subKey)
t = S(t)
t = P(t)
return t
def goRound(l, r, subKey):
return r, binXor(l, Feistel(r, subKey))
def DES(plain, key, method):
subkeys = keyGen(int2bin(key, 64))
if method == 'decrypt':
subkeys = subkeys[::-1]
m = IP(int2bin(plain, 64))
l, r = np.array(m, dtype=int).reshape(2, -1).tolist()
for i in range(16):
l, r = goRound(l, r, subkeys[i])
return bin2int(FP(r + l))
def des_ecb_encrypt(plain_blocks, key):
"""
使用 DES 电子密码本(ECB)模式对明文块列表进行加密。
:param plain_blocks: list[int],64-bit 明文块列表
:param key: int,64-bit 密钥
:return: list[int],加密后的 64-bit 密文块列表
"""
return [DES(block, key, 'encrypt') for block in plain_blocks]
def des_ecb_decrypt(cipher_blocks, key):
return [DES(block, key, 'decrypt') for block in cipher_blocks]
def get_input_blocks():
""" 让用户输入数据,并转换为 64-bit 块 """
data = input("请输入数据(可以是字符串、整数或十六进制):").strip()
if data.startswith("0x"):
blocks = [int(data, 16)]
elif data.isdigit():
blocks = [int(data)]
else:
blocks = pad_data(data)
return blocks
def main():
key = int(input("请输入 64-bit 密钥(16进制):"), 16)
mode = input("请选择模式(encrypt/decrypt):").strip().lower()
if mode == 'encrypt':
plaintext_blocks = get_input_blocks()
cipher_blocks = des_ecb_encrypt(plaintext_blocks, key)
print("加密后:", [hex(c) for c in cipher_blocks])
elif mode == 'decrypt':
cipher_blocks = get_input_blocks()
decrypted_blocks = des_ecb_decrypt(cipher_blocks, key)
try:
print("解密后:", unpad_data(decrypted_blocks))
except:
print("解密后:", [hex(c) for c in decrypted_blocks])
else:
print("无效模式,请输入 'encrypt' 或 'decrypt'")
if __name__ == "__main__":
main()
|
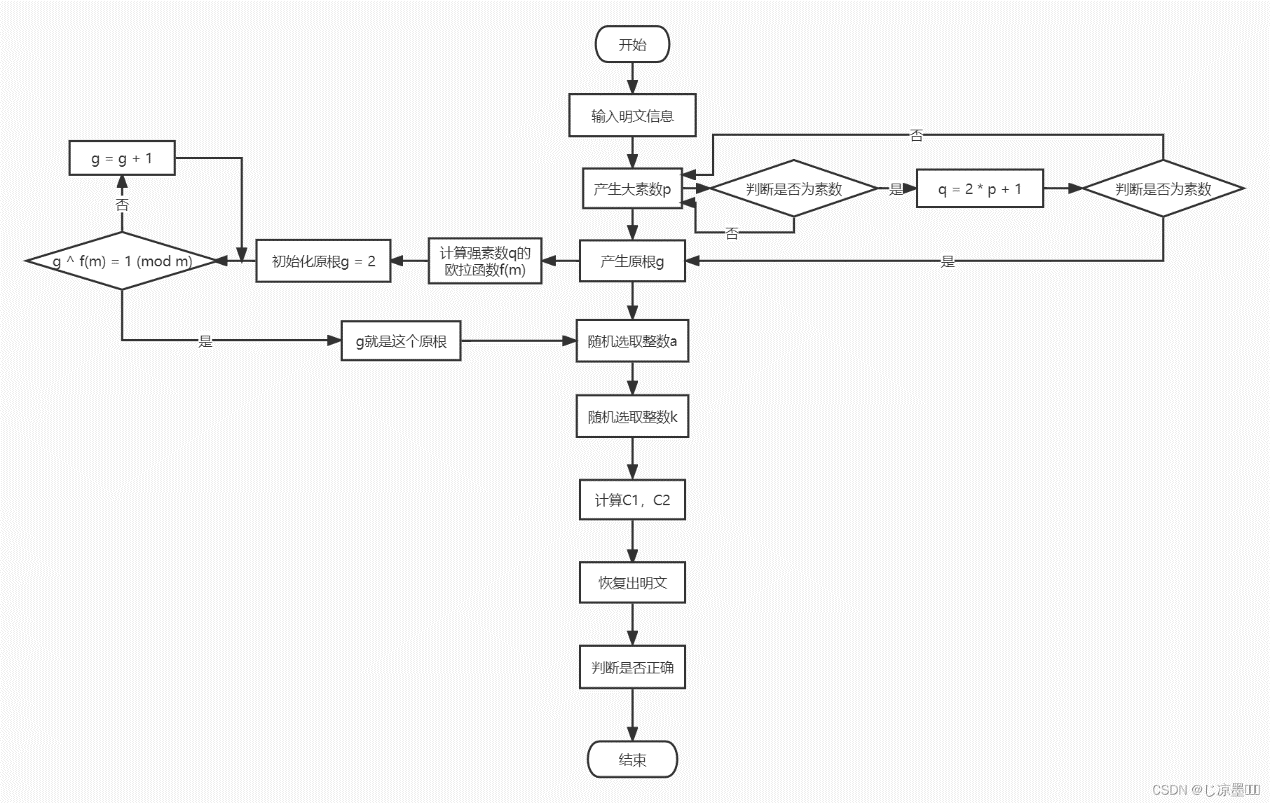

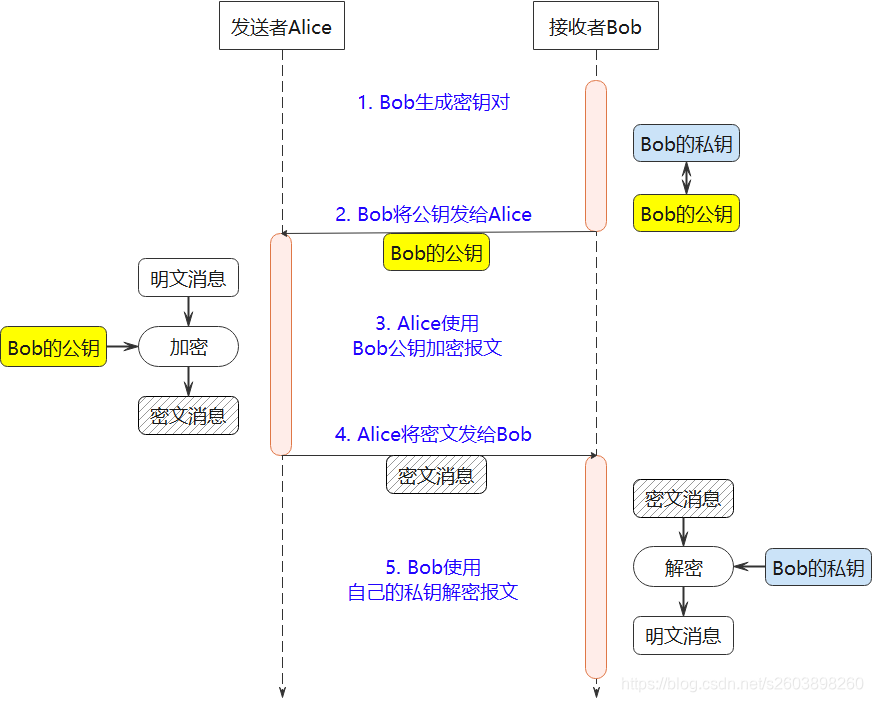

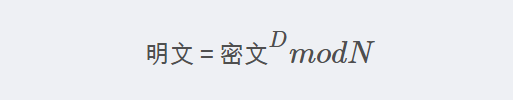
 = (p-1)*(q-1)。【n公开;
= (p-1)*(q-1)。【n公开; ,满足。
,满足。 【e是公开的加密密钥,即E 】
【e是公开的加密密钥,即E 】 。【d是保密的解密密钥】
。【d是保密的解密密钥】 ,其中 d 是奇数(非“奇素数”,只需为奇数)。
,其中 d 是奇数(非“奇素数”,只需为奇数)。 ,此时 s=3 ,d=3。
,此时 s=3 ,d=3。 ,此时 d=1。
,此时 d=1。 。
。 。
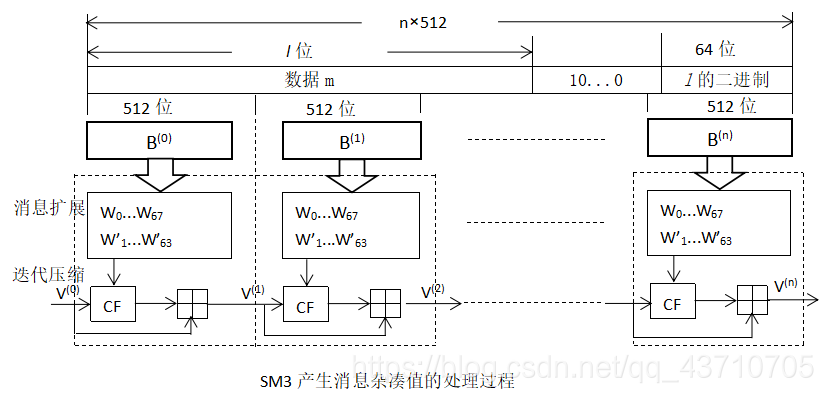
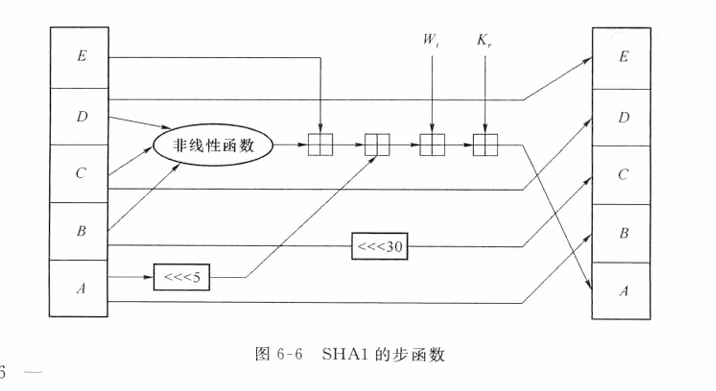
。 比特的信息输入,输出固定长度的128比特(16字节)散列值。
比特的信息输入,输出固定长度的128比特(16字节)散列值。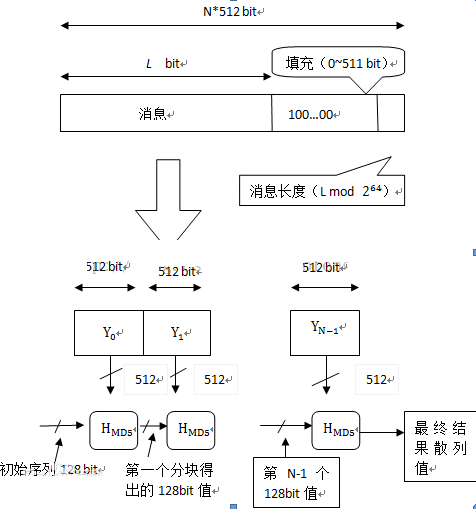
 :代表一个分组
:代表一个分组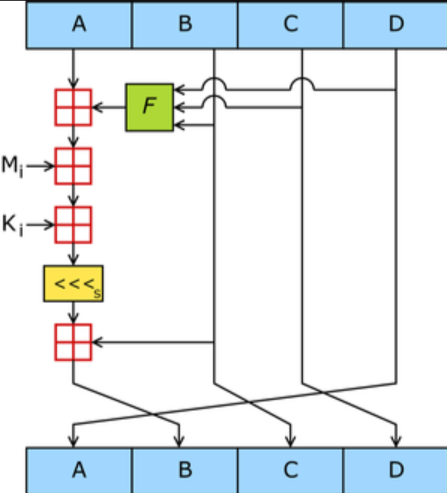

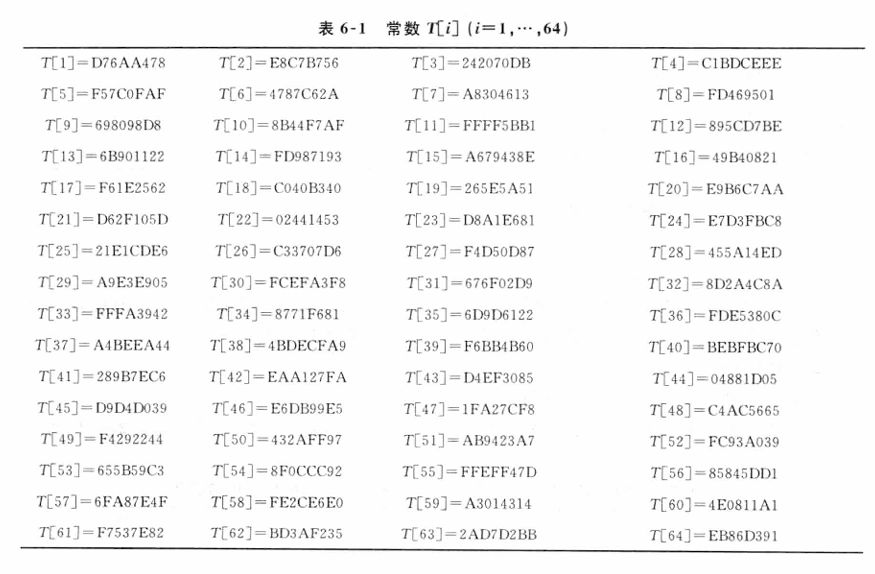
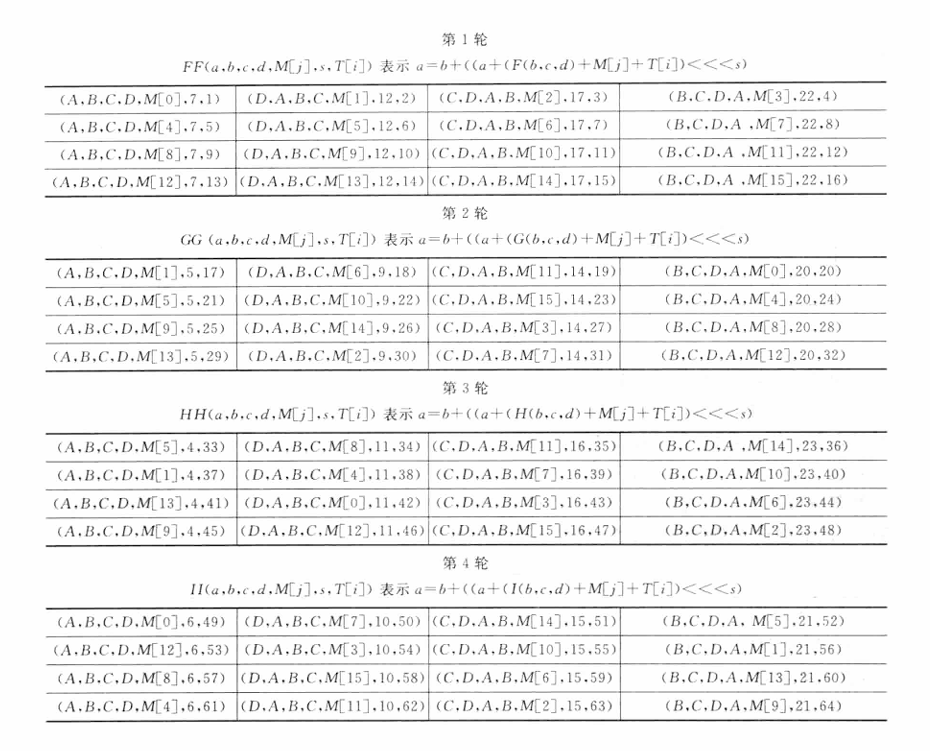


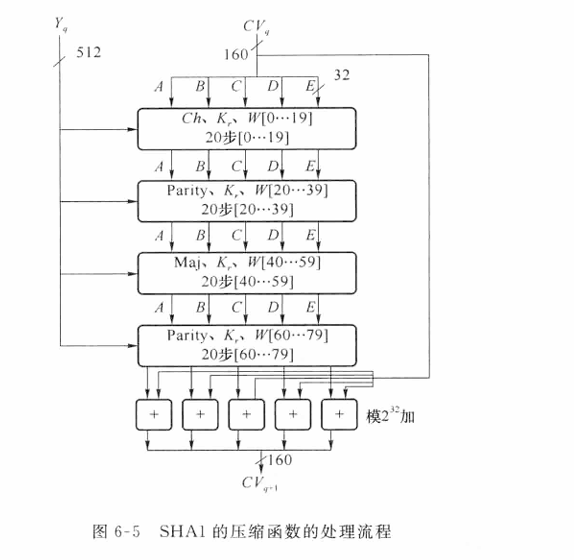



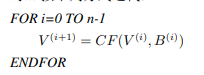

 按以下方法扩展生成132个字
按以下方法扩展生成132个字 , 用于压缩函数CF:
, 用于压缩函数CF: 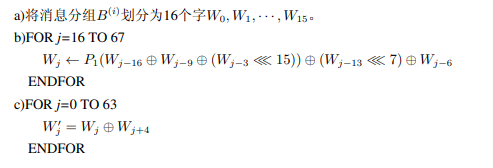

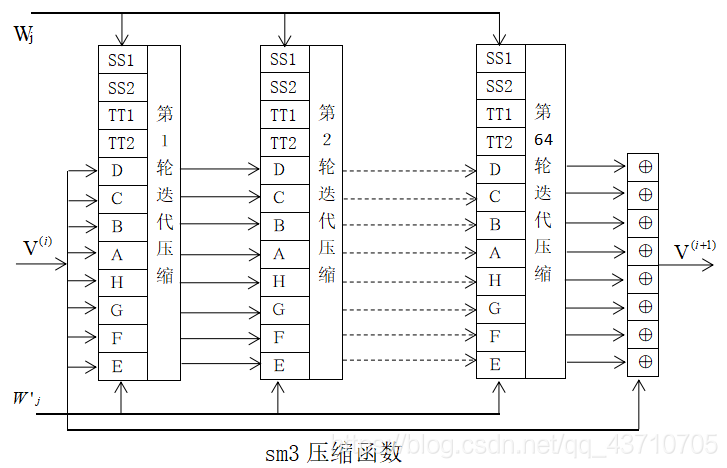
 (X,Y,Z)和
(X,Y,Z)和 (X,Y,Z)是非线性函数,经过循环迭代后提供混淆作用。置换函数
(X,Y,Z)是非线性函数,经过循环迭代后提供混淆作用。置换函数 和
和 是线性函数,经过循环迭代后提供扩散作用,确保算法的安全性。
是线性函数,经过循环迭代后提供扩散作用,确保算法的安全性。