RSA

发表于2025-05-12

一、RSA介绍

RSA加密算法是一种非对称加密算法，所谓非对称，就是指该算法加密和解密使用不同的密钥，即使用加密密钥进行加密、解密密钥进行解密。 在RSA算法中，加密密钥（即公开密钥）PK是公开信息，而解密密钥（即秘密密钥）KR是需要保密的。 加密算法E和解密算法D也都是公开的。

对极大整数做因数分解的难度决定了RSA算法的可靠性。 换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用RSA加密的信息的可靠性就肯定会极度下降。 但找到这样的算法的可能性是非常小的。今天只有短的RSA钥匙才可能被强力方式解破。到目前为止，世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被解破的。

二、RSA算法详解

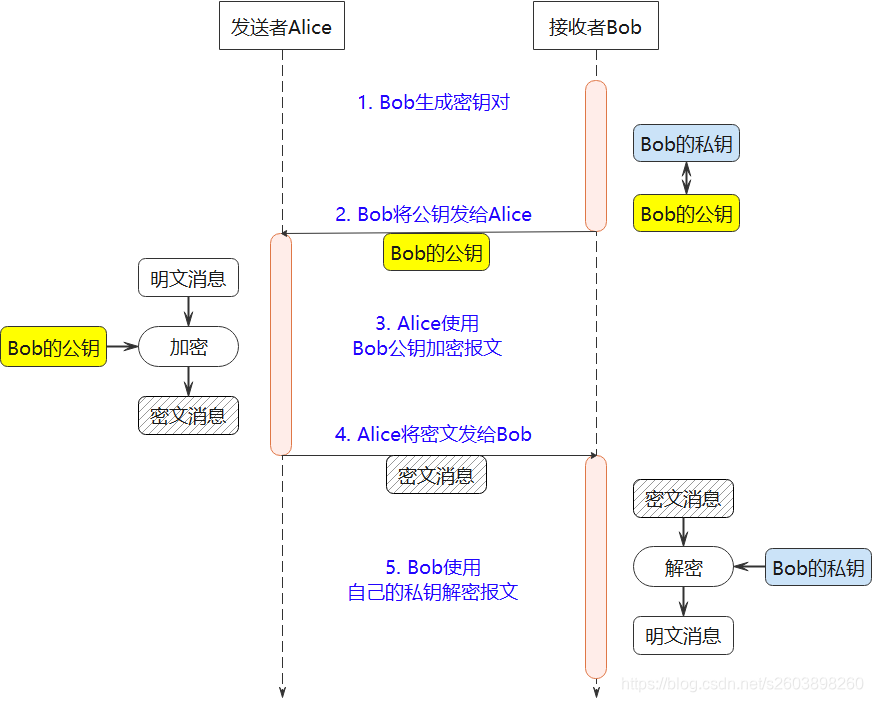
RSA的加密过程可以通过一个公式来表示：

加密：

解密：

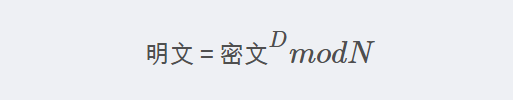
rsa加密的python实现过程

首先要生成两个大素数 p, q (保密)

计算 n=pq，image= (p-1)*(q-1)。【n公开；image即欧拉函数值，需要保密 】

随机选取正整数 image，满足。image【e是公开的加密密钥，即E 】

计算d，满足image。【d是保密的解密密钥】

由此得到公钥(n,e)，私钥 (n,d) 或 (n,p,q)。

加密变换：对于明文 m ，密文为 n。

解密变换：对于密文 c ，明文为 n。

大素数生成

Miller-Rabin 素性检测（Miller-Rabin Primality Test）是一种基于概率的素数检测算法，常用于判断一个大整数是否为素数。它比最基本的试除法效率高得多，是目前实际应用中（比如RSA密钥生成）经常使用的一种方法。

假设我们想检测一个奇数 n>2 是否为素数：

  1. 分解 n−1 的形式
    将 n−1 分解为image，其中 d 是奇数（非“奇素数”，只需为奇数）。
    示例：
    • 若 n=25 ，则 n−1=24=image，此时 s=3 ，d=3。
    • 若 n=9 ，则 n−1=8=image，此时 d=1。
  2. 选择基数 a
    随机选取 a 满足 1<a<n−1 。通常选择多个不同的 a 以提高准确性。
  3. 模幂计算与判定
    • 计算image。
    • 若 x≡1 mod n 或 x≡n−1 mod n：通过当前测试，继续下一轮。
    • 否则：循环平方 x 最多 s−1 次，每次计算 x=x^2 mod n。
      • 若某次得到 x ≡ n−1 mod n，则通过当前测试。
      • 若所有循环后仍未通过，则 n 为合数。
  4. 重复测试
    用不同的 a 重复上述步骤。选择 k 个不同的 a ，可将误判概率降至image。

下面我给出python的代码实现：（部分做了微调） 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 针对随机取得p，q两个数的素性检测     
def miller_rabin_test(n):  # n为要检验得数
    p = n - 1
    r = 0
    # 寻找满足n-1 = 2^s  * m 的s,m两个数
    #  n -1 = 2^r * p
    while p % 2 == 0:  # 最后得到为奇数的p(即m)
        r += 1
        p /= 2
    b = random.randint(2, n - 2)  # 随机取b=（0.n）
    # 如果情况1    b得p次方  与1  同余  mod n
     if fastExpMod(b, p, n) == 1:
        return True  # 通过测试,可能为素数
    # 情况2  b得（2^r  *p）次方  与-1 (n-1) 同余  mod n
    for i in range(7): # 检验六次
        if fastExpMod(b, (2 ** i) * p, n) == n - 1:
            return True  # 如果该数可能为素数，
    return False  # 不可能是素数

这里我们看到在测试的时候，使用到了大数的幂次取模，所以这里我们要先实现大数模的算法，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
# 模N大数的幂乘的快速算法
def fastExpMod(b, e, m):  # 底数，幂，大数N
    result = 1
    e = int(e)   #这里不转化的话，在python3下会出现type error
    while e != 0:
        if e % 2 != 0:  # 按位与
            e -= 1
            result = (result * b) % m
         else:
            e >>= 1
            b = (b * b) % m
    print(f"  快速幂结果: {result}")
    return result

 下面给出大素数生成的代码吧：（上面的重复内容不再写出）

1
2
3
4
5
6
7
8
9
10
11
12
13
# 生成大素数：
def create_prime_num(bits):
    print(f"\n开始生成 {bits} 位大素数：")
    while True:
            # 如果经过10次素性检测，那么很大概率上，这个数就是素数
           n = random.randint(2 ** (int(bits) - 1), 2 ** int(bits) - 1)
            if n % 2 != 0:
            print(f"  尝试候选数: {n}")
            if all(miller_rabin_test(n) for _ in range(5)):
                print(f"  >>> 确认素数: {n}\n")
                return n
            else:
                print(f"  非素数，重新尝试...\n")

我们得到生成的大素数之后，就比较简单了。

生成密钥

这里直接给出代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 生成密钥（包括公钥和私钥）
def create_keys(keylength):
    p = create_prime_num(keylength // 2)
    q = create_prime_num(keylength // 2)
    n = p * q
    fn = (p - 1) * (q - 1)
    e = selectE(fn)
    d = match_d(e, fn)
    return (n, e, d)

# 选择加密指数 e
def selectE(fn):
    while True:
        e = random.randint(2, fn - 1)
        if math.gcd(e, fn) == 1:
            return e

# 根据选择的e，匹配出唯一的d
def match_d(e, fn):
    def extended_gcd(a, b):
        if b == 0:
            return (1, 0)
        else:
            x1, y1 = extended_gcd(b, a % b)
            x, y = y1, x1 - (a // b) * y1
            return (x, y)
    x, _ = extended_gcd(e, fn)
    return x % fn

至此我们得到了公钥和私钥。

加解密实现

1
2
3
4
5
6
#加密
def encrypt(M, e, n):
    return fastExpMod(M, e, n)
#解密
def decrypt( C, d, m):
    return fastExpMod(C, d, m)

测试结果

可以完成读取文本的加密，注意标点符号如果是中文的标点，会出现乱码，但不会影响信息的读取。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
import random
import math

# 快速模幂运算
def fastExpMod(b, e, m):
    result = 1
    e = int(e)
    while e != 0:
        if e % 2 != 0:
            e -= 1
            result = (result * b) % m
            continue
        e >>= 1
        b = (b * b) % m
    return result

# Miller-Rabin 素性检测
def miller_rabin_test(n):
    p = n - 1
    r = 0
    while p % 2 == 0:
        r += 1
        p //= 2  # 确保是整数
    b = random.randint(2, n - 2)
    if fastExpMod(b, p, n) == 1:
        return True
    for i in range(7):
        if fastExpMod(b, (2 ** i) * p, n) == n - 1:
            return True
    return False

# 生成大素数
def create_prime_num(bits):
    while True:
        n = random.randint(2 ** (int(bits) - 1), 2 ** int(bits) - 1)
        if n % 2 != 0:
            if all(miller_rabin_test(n) for _ in range(10)):
                return n

# 生成密钥对
def create_keys(keylength):
    p = create_prime_num(keylength // 2)
    q = create_prime_num(keylength // 2)
    n = p * q
    fn = (p - 1) * (q - 1)
    e = selectE(fn)
    d = match_d(e, fn)
    return (n, e, d)

# 选择加密指数 e
def selectE(fn):
    while True:
        e = random.randint(2, fn - 1)
        if math.gcd(e, fn) == 1:
            return e

# 计算解密指数 d
def match_d(e, fn):
    def extended_gcd(a, b):
        if b == 0:
            return (1, 0)
        else:
            x1, y1 = extended_gcd(b, a % b)
            x, y = y1, x1 - (a // b) * y1
            return (x, y)
    x, _ = extended_gcd(e, fn)
    return x % fn

# 加解密函数
def encrypt(M, e, n):
    return fastExpMod(M, e, n)

def decrypt(C, d, n):
    return fastExpMod(C, d, n)

# 交互菜单
def display():
    print("_________________RSA_________________")
    print("1. 加密 Encrypt")
    print("2. 解密 Decrypt")
    print("q. 退出 Quit")
    print("_____________________________________")

# 主函数
def main():
    while True:
        display()
        choice = input("请选择操作: ").strip().lower()

        if choice == '1':
            plaintext = input("请输入要加密的明文（支持中文）: ")
            n, e, d = create_keys(16)  # 密钥长度可改为更大
            print(f"\n生成的公钥: (n={n}, e={e})")
            print(f"请妥善保存私钥以解密: (n={n}, d={d})")

            encrypted_list = [encrypt(ord(ch), e, n) for ch in plaintext]
            print(f"\n加密结果（密文整数列表）: {encrypted_list}\n")

        elif choice == '2':
            try:
                n, d = map(int, input("请输入私钥（格式: n d）: ").split())
                encrypted_input = input("请输入密文（整数列表，例如：[123, 456]）: ")
                encrypted_list = eval(encrypted_input)

                decrypted = ''.join([chr(decrypt(c, d, n)) for c in encrypted_list])
                print(f"\n解密结果: {decrypted}\n")
            except Exception as e:
                print(f"解密出错: {e}\n")

        elif choice == 'q':
            print("退出程序")
            break
        else:
            print("无效选项，请重新输入。\n")

if __name__ == '__main__':
    main()

RSA.py

RSA_1.py